G2R2: A True R-squared Measure for Linear and Non-Linear Predictive Models

Abstract

This paper introduces a framework that allows us to construct an all-purpose true R-squared measure, G2R2. Unlike the other measures purported to be R-Squared type, it maintains all the desirable attributes of the Ordinary Least Squares (OLS) R-squared and also allows the analyst to make statistical inferences about the predictive power of competing models. In addition, it is universally appropriate for all models— linear, non-linear, parametric and non-parametric models. SAS codes to estimate G2R2 and its variance from data are available upon request.

Introduction

After fitting a predictive model, a data scientist has to assess its predictive power. R-squared has been a desirable measure of fit for linear models: As the proportion of total variation of the dependent variable explained by the model, it has a logical relationship with model fit; it’s nicely bounded between 0 (no fit) and 1 (perfect fit); and its asymptotic distribution can be easily derived to make inferences about differences in model fits. The only shortcoming of R-squared is that it was constructed from and for only linear models.

Unfortunately, all attempts to create a fit measure of universal use have come at the sacrifice of transparency and other desirable qualities. Many of the substitute measures such as Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), to mention a couple, are based on probability densities (likelihood values) and are hence less intuitive. In addition, the substitutes require the modeler to know the true distribution of the dependent variable—an impractical prescience! And lastly, their finite sample or even asymptotic properties are less understood. Even the measures tailored to look like R-squared suffer similar deficiencies: the generalized R-squared measure proposed by Cox and Snell (1989) , and Magee(1990) are baked from likelihood values; Cameron and Windmeijer (1997) propose a measure they consider as R-squared-type, but is based on Kullback-Liebler divergence (an entropy metric) and only applies to a class of exponential family regression models.

In this paper, I construct a true R-squared measure, G2R2, which is based on variances, preserves all the desirable characteristics of R-squared, and above all, can be used to assess all models, linear and non-linear. In the linear case, G2R2 and the Ordinary Least Squares Regression (OLS) R-squared are identical. The paper is structured as follows: Part 1 constructs G2R2; part 2 discusses its properties; part 3 derives its distribution; part 4 highlights application traps of G2R2; and part 5 validates a simulated non-linear model with G2R2.

Part 1: Constructing G2R2

The linear R-squared is derived from standard OLS assumptions, particularly the additive assumption which stipulates that the error term is additive and uncorrelated with the model variables (X). This allows the dependent variable, Y, to be expressed as the sum of its conditional mean E(Y|X) and error term; and consequently, the variance of Y as the sum of variances of the conditional expectation and error term. Hence, R-squared—the proportion of the variance Y accounted for by the conditional mean—is calculated as the ratio of the variance of the conditional mean to that of the dependent variable.

However, we don’t need these assumptions (either the linearity, additivity or any other) to express the variance of the dependent variable as the sum of the variances of the predictions and the errors. In fact the law of total variance allows us to compartmentalize the variance of Y as the sum of the variances of its conditional mean and process errors with no such restrictive assumptions:

$Var(Y)=Var(E(Y|X))+E(Var(Y|X))---(1)$

It’s easy to see from (1) that statistically predictive variables will increase the variance of conditional mean,Var(E(Y|X)), and decrease that of the error, E(Var(Y|X)): If the model variables fully explain Y, the variance of the conditional mean is equal to the variance of the dependent variable. Alternatively, if there is no statistically significant model variable, the variance of the conditional mean is 0 and all variations in the dependent variable are rather carried by the process error. G2R2 therefore measures the efficacy of a predictive model as the ratio of the variance of its conditional mean to that of its dependent variable:

$G2R2=\frac{Var(E(Y|X))}{Var(Y)}=\frac{\sigma_{\widehat{Y}}^{2}}{\sigma_{Y}^{2}}---(2a)$

Or Equivalently,

$G2R2=1-\frac{E(Var(Y|X))}{Var(Y)}---(2b)$

The sample statistic, g2r2, is estimated as:

$g2r2=\frac{\sum_{i}^{N}(\widehat{Y_{i}}-\overline{Y})^{2}}{\sum_{i}^{N}(Y_{i}-\overline{Y})^{2}}=\frac{s_{\widehat{Y}}^2}{s_{Y}^{2}}---(3)$ ¹

where:

N is the sample size;

Y_i is the observed value of the dependent variable for the ith observation;

$\widehat{Y_i}$ is the predicted value, E(Y|X), for the ith observation;

$\overline{Y}=\frac{\sum_{i}^{N}Y_{i}}{N}$

Despite the similarity between the formulas of G2R2 and OLS R-squared, the reader should appreciate the comprehensiveness and distinctiveness of the new measure. When the model is linear, the two measures are the same; when non-linear, the new framework authorizes the use of the ratio of variance of predicted variable to that of dependent variable as legitimate measure of fit. However, in the non-linear case, G2R2 has some operational differences. For instance, the variance of the error is not necessarily computed as the variance of the difference between the observed and predicted values of the dependent variable, i.e. $\inline Var(Y-\widehat{Y})$ . For instance, for models with multiplicative effects and errors, the error term is rather calculated as the quotient of the observed and predicted values. To distinguish this new measure from the OLS R-squared, I have named it G2R2 (as in the Generation 2 R-squared).

Part 2: Properties of G2R2

The merit of G2R2 is that it maintains the desirable qualities of the OLS R-squared and builds on its shortcomings. We discuss some of the qualities below:

As an artifact of equation (1), it is applicable to all modeling frameworks, linear or non-linear.
It is also non-parametric and requires of the user no knowledge of the distribution of the dependent variable. Unfortunately, most of the likelihood based measures demands such prescience.
It has a logical relationship with model fit. The more predictive the model variables are, the higher the variance of the predicted means and G2R2.
It ranges from 0 to 1. A model with no statistically significant variable has G2R2 of 0, and a model whose variables fully explain Y has a G2R2 of 1. This is easy to see from (1). Because competing measures like AIC and BIC lack such confined range, it’s hard for the scientist to gauge the model’s proximity to perfect or useless.
Its asymptotic distribution can be easily derived to make inferences about its sample estimates. In fact, we discuss this further in the next section.

Part 3: The Asymptotic Distribution of G2R2

Because G2R2 is composed of familiar moments, its distribution is easily derivable: By Slutsky’s Theorem,

$\inline g2r2=\frac{s_{\widehat{Y}}^2}{s_{Y}^{2}}\rightarrow G2R2=\frac{\sigma_{\widehat{Y}}^2}{\sigma_{Y}^{2}}---(4)$

The variance of g2r2 can be derived using the delta method as:

$\inline Var\left ( \frac{s_{\widehat{Y}}^{2}}{s_{Y}^{2}} \right )\cong \frac{\sigma _{\widehat{Y}}^{4}}{\sigma _{Y}^{4}} \left ( \frac{\mu _{4,\widehat{Y}}}{N\sigma _{\widehat{Y}}^{4}} +\frac{\mu _{4,Y}}{N\sigma _{Y}^{4}}-\frac{2}{N}-\frac{2Cov(s_{\widehat{Y}}^{2},s_{Y}^{2})}{\sigma _{\widehat{Y}}^{2}\sigma_{Y}^{2}}\right )---(5)^2$

Where:

$\inline \sigma_{Y}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(Y_{i}-\overline{Y})^{2}},\sigma_{\widehat{Y}}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(\widehat{Y}_{i}-\overline{Y})^{2}}$

$\mu_{4,Y}=\frac{1}{N}\sum_{i=1}^{N}(Y_{i}-\overline{Y})^{4},\mu_{4,\widehat{Y}}=\frac{1}{N}\sum_{i=1}^{N}(\widehat{Y}_{i}-\overline{Y})^{4}$

$\inline Cov(s_{\widehat{Y}}^{2},s_{Y}^{2})=\left ( \frac{1}{N^2} \sum_{i=1}^{N}E[(\widehat{Y_i}-\overline{Y})^2(Y_i-\overline{Y})^2]\right )-\frac{\sigma_{\widehat{Y}}^{2}\sigma_{Y}^{2}}{N}---(6)$

Details of the derivation of (5) and (6) can be provided upon request.

(4), (5) and Central Limit Theory imply that g2r2 follows a normal distribution with mean $\inline \frac{\sigma_{\widehat{Y}}^{2}}{\sigma_{Y}^{2}}$ , and variance $\inline \frac{\sigma _{\widehat{Y}}^{4}}{\sigma _{Y}^{4}} \left ( \frac{\mu _{4,\widehat{Y}}}{N\sigma _{\widehat{Y}}^{4}} +\frac{\mu _{4,Y}}{N\sigma _{Y}^{4}}-\frac{2}{N}-\frac{2Cov(s_{\widehat{Y}}^{2},s_{Y}^{2})}{\sigma _{\widehat{Y}}^{2}\sigma_{Y}^{2}}\right )$ .

And with this result, the modeler will no longer have to evaluate models blindly (i.e. compare differences in measures of model fit without knowing whether the differences are statistically significant or not). He can assess and make statistical inference about the fit of competing models. The SAS code for computing this variance can be provided upon request.

Part 4: Practical Notes About G2R2

G2R2 as a ratio of variances vis-à-vis standard deviations can mull otherwise statistically significant differences in fits between competing models: Squaring a fraction—ratio of standard deviations—diminishes their magnitudes and scale. The modeler should therefore use statistical distribution of g2r2 (both magnitude and variance) derived in part 2, and not merely the magnitude, to make inferences about the differences in predictive powers of models. However, he may choose to rather report the square root of g2r2 to his non-technical audience: Square root function will amplify the differences in model fit without distorting the order of their magnitudes.

Also, G2R2 does not have a penalty for model complexity (number of variables). Hence, the modeler has to beware of over-fitting when he does in-sample model validation. In the case of out of sample validation, G2R2 as defined in (2a) can be artificially increased by selecting parameter values that are higher in absolute value than the fitted parameters. Hence, when a subset of the model parameters is selected, the modeler should rather calculate g2r2 as the difference between unity and the ratio of the variance of the model error to that of actual outcomes of the dependent variable as specified in 2b. That way, any inaccuracies in the predictions will be captured in E(Var(Y|X)), and hence accordingly reduce g2r2. In a multiplicative model, the modeler should be sure the error term (ratio of actual to predicted outcomes) is not heteroscedastic before using specification 2b³.

The reader should note that g2r2 computed from 2a and 2b on an out-of-sample validation data will have the same mean but different variances. This result is shown by the simulation exercise in part 5.

Part 5: Validating a Simulated Non-Linear Model with G2R2

Consider the following non-linear model:

$Y=0.3X_1^{0.5}X_2^{0.25}\varepsilon ---(7)$

where:

Y is the dependent variable;

X₁ and X₂ are observed covariates distributed as i.i.d. uniform (0,1); and

$\varepsilon$ is the unobserved exogenous error also with uniform(0,1) distribution.

With a little algebra, V(E(Y|X)) and EV(Y|X) can be shown to equal 0.0011 and 0.0025 respectively; which means the theoretical G2R2 equals 0.3056.

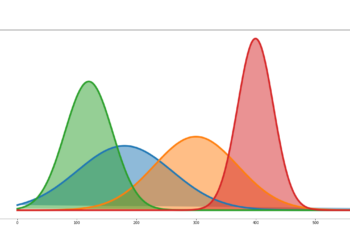
I simulate the above model 250 times, with each trial having a sample size of 1000 independent observations. For each trial, I calculate the sample g2r2 using equations (2a) and (2b). The respective distributions observed are as follows:

As can be seen from the above exhibits, the means of the sample g2r2s generated by the two methods are statistically the same as that of the theoretical G2R2. This is corroborating evidence that the sample g2r2 is a consistent estimator of the true G2R2, and a viable measure of the predictive power for all (including non-linear) models. Despite their equal means, the variances of the two methods are different. The user should therefore be cognizant of this fact when making statistical inferences about model fit with G2R2. Since this fact is not obvious to even frequent users of the OLS R-squared, I wrote a paper to create awareness: See Two Notes About the Two Faces of R-Squared (https://gkdblog.com/two-notes-about-the-two-faces-of-r-squared/).

Footnotes

The mean of the dependent variable should be equal to the mean of the predictions to ascertain the two are of the same scale. Otherwise, one must be multiplied by constant to attain this result.
Because G2R2 is a convex function(ratio) of variances, its variance approximated by the delta method will be underestimated.
This note is particularly relevant to Generalized Linear Models with log-link. In the case where the error is heteroscedastic, specification 2a should be used.